More on 3x+1 Completeness
Although there is no really hard evidence, data currently available suggests
that the completeness is limited to a value below the limit of
ln(2) / ln(3) = 0.6309...
There are two arguments to support this view. Both of them were originally
contributed by Eric Farin.
The first argument is based on current data. From the general formula
E.ln(2) = O.ln(3) + ln(N) + ln(Res)
through substitution of O = E.C we reach
E.ln(2) = E.C.ln(3) + ln(N) + ln(Res)
which on regrouping yields
ln(2) - C.ln(3) = ( ln(N) + ln(Res) ) / E
Therefore, if C is to get close to the theoretical limit we expect E/ln(N)
(commonly known as Gamma) to be divergent. The class records found thus far
however are showing a radically different picture, as can be seen from this curve
of E/ln(N) for all Class Records up to 8000:
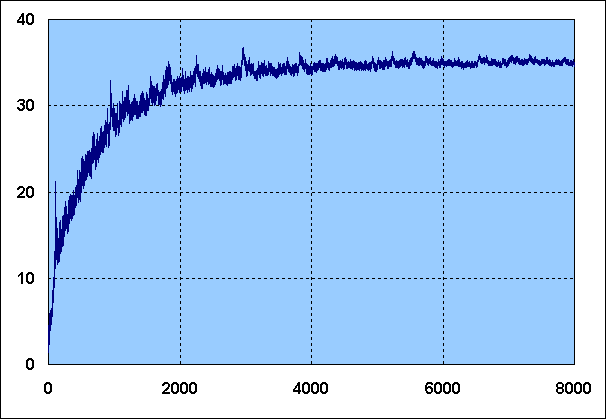
Class records up to ± 2200 are either exact, or else correct within an
order of magnitude (i.e. no more than a factor 6 too high). For higher class records
current "best known candidates" are depicted. Beyond 2200 the values are therefore less
and less certain, although empirical evidence suggests most of them
are probably not too far from the exact values.
The curve apparently shows a tendency to converge to a value roughly somewhere
between 35 and 45. This appears to indicate that Gamma is bound, and therefore that
the Completeness will not get infinitesimally close to its theoretical limit.
The second argument is a statistical one. From every number N within a Delay Class x
we can derive a number 2N in Delay Class x+1 plus possibly another one if N is of
the form 6k+4, in which case 2k+1 has also Delay x+1. In the first case the number has
one more even step, in the latter case it has one more odd step. We can therefore
approach the number of members having O odd steps in any Delay Class D by
( D! / ( (D-O)! . O! ) ) . (1/3)O
Since we know the completeness of a number once D and O are known we
can estimate how many numbers exist having a specific Completeness C.
Using the Stirling formula for
N! = sqrt(2.π.N) . (N/e)N
we eventually find that the log of the number is approached by
C.ln(C) + (1-C).ln(1-C) + C.ln(3)
We can therefore state a number with a specific Completeness C can only exist
if the expression above is positive. Setting the expression equal to zero and
solving for C yields C = 0.6090897679... which therefore seems to indicate the
Completeness will not reach its theoretical maximum value of 0.6309... The current
maximum value found is 0.606274... which supports the number above.
Thus there appears to be some evidence to support
- Conjecture 3:
- A number Cmax exists such that for all N
C(N) < Cmax.
with Cmax < ln(2) / ln(3).
If the constant mentioned above is indeed the correct value a simple calculation
shows that the maximum value for Gamma will be 41.677647656...
The data on Gamma records show that values really close
to this constant have so far not been observed though.
Back to the general 3x+1 page.

